games-on-graphs | Michael Levet

I. Introduction
This blog entry will briefly introduce notions from game theory to explore a traffic routing game. I assume familiarity with basic notions from graph theory; in particular, the directed graph.

II. Preliminaries
This section will introduce basic notions of game theory. Let’s begin with the definition of a game.

Game: A game in normal (strategic) form is defined as a three-tuple $[N, (S_{i})_{i \in N}, (u_{i})_{i \in N}]$ , where $N$ is the set of players, $S_{i}$ is player $i$ ‘s set of strategies, and $u_{i} : \prod_{i \in N} S_{i} \to \mathbb{R}$ is player $i$ ‘s utility function.

Conceptually, each player can do something (i.e., choose a strategy). Each player’s payoff (or utility) depends on his or her own action, as well as the actions of the other players. The goal for each player is to maximize his or her utility.

Normal form games are games of perfect information. That is, each player has complete knowledge of the options and payoffs of each option. The players also move simultaneously in normal form games.

The Prisoner’s Dilemma is the classic example of a (normal form) game. The story behind the Prisoner’s Dilemma is this. There are two prisoners being held in separate rooms for police interrogation. These players are both offered a plea deal. In return for confessing and implicating the other player, the given prisoner is given a reduced sentence of one year so long as the other player did not confess. The player that stayed quiet gets a ten year prison sentence. If both players confess, they each get five years in prison. If they both stay quiet, they each get only two years in prison. The police inform each prisoner that their counterpart is receiving the same offer. Thus, this is a simultaneous move game of perfect information.

The table representation of the Prisoner’s Dilemma is provided below.

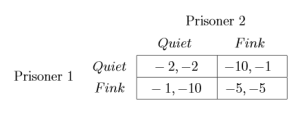
Prisoner one’s options are listed on the left-hand side while prisoner two’s options are listed on the top of the table. The payoffs in each cell list the payoffs in player order. So if player one chooses to Fink and player two chooses to keep Quiet, the strategy history is (Fink, Quiet) with payoff $(-1, -10)$ . That is, prisoner one gets one year in prison and prisoner two gets ten years in prison.

Formally, the Prisoner’s Dilemma can be written using the definition of a game. We have player set $N = \{1, 2\}$ with strategies $S_{i} = \{ \text{Fink}, \text{Quiet} \}$ for each $i \in N$ . The utility function for each player is given by the table above. We have $u_{i}(\text{Quiet}, \text{Quiet}) = -2$ and $u_{i}(\text{Fink}, \text{Fink}) = -5$ for each player $i \in N$ . Finally, $u_{1}(\text{Fink}, \text{Quiet}) = u_{2}(\text{Quiet}, \text{Fink}) = -1$ and $u_{1}(\text{Quiet}, \text{Fink}) = u_{2}(\text{Fink}, \text{Quiet}) = -10.$

Remark: Let $G[N, (S_{i})_{i \in N}, (u_{i})_{i \in N}]$ be a game and let $i \in N$ . Then $-i$ refers to the set $N \setminus \{i\}$ , and so $S_{-i} = \prod_{j \in N \setminus{i} } S_{j}$ . That is, $-i$ refers to the set of players other than $i$ .

Remark: It is important to note that in the above example, the strategies are very straight-forward. In more complicated games, decision structures can be included in the strategies. That is, think of a strategy like an algorithm.

The notion of a Nash Equilibrium will now be introduced to help determine the outcomes of games.

Nash Equilibrium: Let $G[N, (S_{i})_{i \in N}, (u_{i})_{i \in N}]$ be a game and let $s^{*} = (s_{i}^{*})_{i \in N}, s_{i}^{*} \in S_{i}$ be a joint strategy. Then $s^{*}$ is a Nash Equilibrium if the following condition is satisfied:

For every $i \in N$ , $u_{i}(s_{i}^{*}, s_{-i}^{*}) \geq u_{i}(s_{i}, s_{-i}^{*})$ for all $s_{i} \in S_{i}$ .

In other words, no player can improve his or her payoff by unilaterally deviating. This concept will be illustrated with the following claim.

Claim: The only Nash Equilibrium of the Prisoner’s Dilemma is (Fink, Fink).

Proof: This claim will be proven directly. It will first be shown that (Fink, Fink) is a Nash Equilibrium. If prisoner one changes his or her strategy to Quiet, then $u_{1}(\text{Quiet}, \text{Fink}) = -10 < u_{1}(\text{Fink}, \text{Fink}) = -5$ . So prisoner one will not deviate. By similar argument, prisoner two will not deviate. So (Fink, Fink) is a Nash Equilibrium.

It will now be shown that (Fink, Fink) is the unique Nash Equilibrium. Suppose there exists a second Nash Equilibrium. We have three options to consider (Quiet, Quiet), (Fink, Quiet), and (Quiet, Fink). Suppose (Quiet, Quiet) is a Nash Equilibrium. Then each player has incentive to Fink, as $u_{i}(\text{Fink}, \text{Quiet}) = -1 \geq u_{i}(\text{Quiet}, \text{Quiet})$ . So (Quiet, Quiet) is not a Nash Equilibrium. Suppose instead (Fink, Quiet) is a Nash Equilibrium. Then prisoner two has incentive to deviate and Fink, raising his payoff to $-5$ from $-10$ . By symmetry, (Quiet, Fink) is not a Nash Equilibrium. It follows that (Fink, Fink) is the unique Nash Equilibrium. QED.

Remark: Not every game has a unique Nash Equilibrium, and there exist games without any Nash Equilibria.

Next, the concept of a Mixed-Strategy and Mixed-Strategy Nash Equilibrium are defined.

Mixed-Strategies: A mixed-strategy is a probability distribution $\sigma_{i} : S_{i} \to [0, 1]$ such that $\sum_{s_{i} \in S_{i}} \sigma_{i}(s_{i}) = 1$ . The set $\Sigma_{i}$ denotes the mixed strategies of player $i$ .

Mixed-Strategies Nash Equilibrium: Let $\sigma^{*} = (\sigma_{1}^{*}, ..., \sigma_{n}^{*})$ be a mixed strategy profile. Then $\sigma^{*}$ is a Mixed-Strategies Nash Equilibrium if and only if, for every player $i \in N$ , the following two conditions hold:

For every pure strategy $s_{i}$ with $\sigma_{i}(s_{i}) > 0$ , $u_{i}(s_{i}, \sigma_{-i}^{*}) = u_{i}(\sigma^{*})$ .
For every pure strategy $s_{i}$ with $\sigma_{i}(s_{i}) = 0$ , $u_{i}(s_{i}, \sigma_{-i}^{*}) \leq u_{i}(\sigma^{*})$ .

I introduce a final theorem, which justifies the existence of a Nash Equilibrium in a finite, normal form game.

Theorem (Nash): Every finite normal form game has a Nash Equilibrium, possibly in mixed strategies.

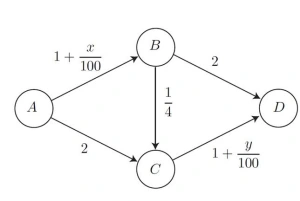
III. A Network Routing Game
The problem in question deals with the following network. The variable $x$ is defined to be the number of players using the directed edge $(A, B)$ , and the variable $y$ is defined to be the number of players using the directed edge $(C, D)$ . The weight of each directed edge correspond to latency time or cost. Players seek to travel from the source vertex $A$ to the destination vertex $D$ , minimizing the total cost or latency.

Observe that there are three possible routes a player may take: ABD, ACD, and ABCD. Let $n_{1}$ denote the number of players taking route ABD, $n_{2}$ denote the number of players taking route ACD, and $n_{3}$ denote the number of players taking route ABCD. Let $n := n_{1} + n_{2} + n_{3} = 100$ . We examine a few claims regarding this game.

Claim 1: Let $n_{1} = n_{2} = 25$ and $n_{3} = 50$ . This is a Nash Equilibrium.

Proof: This claim will be proven directly. To show there is a Nash equilibrium, we show that no player can unilaterally deviate and improve his situation. When $n_1 = n_2 = 25$ and $n_3=50$ , the edges $(A,B),(C,D)$ have weight $1.75$ . So suppose an ABD player chooses ACD instead. Then that player is adding $1$ to $y$ , which increases the cost of using the edge (C,D) to $1.76$ and in turn, increasing his cost of using that route. So an ABD player will not deviate to ACD. By symmetry, an ACD player will similarly not switch to ABD. If an ABD or ACD player chooses ABCD instead, then his cost becomes $3.76$ , where as staying yields a cost of $3.75$ . So no ACD and ABD players will deviate.

Now suppose an ABCD player deviates to either ABD or ACD. On the ABCD route, this player contributes $\frac{1}{100}$ to the cost of the $(A,B)$ and $(C,D)$ edges. So whichever edge he uses, he still incurs that marginal cost. The $\frac{1}{4}$ from the $(B,C)$ edge lost, but then the $(A,C)$ and $(B,D)$ edges have a cost of $2 > 1.75$ . So the total cost of switching is $1.75 + 2 = 1.75 + .25 + 1.75$ which is the cost of keeping the ABCD route, and so there is no incentive to switch. Thus, $n_1 = n_2 = 25$ and $n_3 = 50$ is a Nash equilibrium. QED.

Claim 2: There exists a joint strategy in which all players are better off than in Claim 1, but such a configuration is not a Nash Equilibrium.

Proof: This claim will be proven directly. Let $n_{1} = n_{2} = 50$ . Then each player incurs a latency cost of $3.50 < 3.75$ , so all players are better off. In order to show this joint strategy is not a Nash Equilibrium, it suffices to show a single player can unilaterally deviate and decrease his cost. Let a player using the ABD route instead choose the ABCD route. Then this player incurs a latency cost of $1.50 + 1.51 + 0.25 = 3.26 < 3.50$ . By similar argument, a player using the ACD route could also deviate to ABCD incurring the same latency cost of $3.26 < 3.50$ . And so the joint strategy $n_{1} = n_{2} = 50$ is not a Nash Equilibrium. QED.

Remark: Observe that Claim 2 mirrors the Prisoner’s Dilemma game. In the Prisoner’s Dilemma game, the two prisoners can better their situations by keeping quiet. However, one prisoner can then further improve his situation by unilaterally deviating and finking.

Claim 3: There exists a Nash Equilibrium in which all players use the same strategy.

Proof: This claim will be proven directly. Observe that this game is finite and in normal form. Therefore, a Nash Equilibrium exists by Nash’s theorem. Claim 1 provides a Nash Equilibrium, but not one in which all players use the same strategies. However, the distributions of each strategy from Claim 1 provide for a Mixed Strategies Nash Equilibrium. For each player $i \in N$ , let the strategy be $\sigma_{i}(n_{1}) = \sigma_{i}(n_{2}) = 0.25$ and $\sigma_{i}(n_{3}) = 0.50$ .

It suffices to show that $\Sigma_{i}$ is a Mixed Strategies Nash Equilibrium. Suppose player $i$ chooses ABD. Then under $\sigma_{-1}^{*}$ , the proportion of choosing ABD is $\frac{24}{99}$ , the proportion of choosing ACD is $\frac{25}{99}$ and the proportion of choosing ABCD is $\frac{50}{99}$ . So $\mathbb{E}[u_{i}(\text{ABD}, \sigma_{-i}^{*})] = 1 + \frac{74 + 1}{100} + 2 = 3.75 = \mathbb{E}[u_{i}(\sigma^{*})]$ . By similar arguments, $\mathbb{E}[u_{i}(\text{ACD}, \sigma_{-i}^{*})] = \mathbb{E}[u_{i}(\sigma^{*})] = 3.75$ and $\mathbb{E}[u_{i}(\text{ABD}, \sigma_{-i}^{*})] = \mathbb{E}[u_{i}(\sigma^{*})] = 3.75$ . By the analysis in Claim 1, no player will want to deviate. And so this is a symmetric mixed strategies Nash Equilibrium. QED.